The current web calculator for stopping powers is a real time implemetation of the "SRIM Module.exe" (with an upper energy limit of 5 GeV/amu) included in SRIM 2013 code (SRIM Tutorials) - whose maximum available energy is 10 GeV/amu -, i.e., the used electronic stopping power tables are those provided by "SRIM Module.exe" code with a low energy limit of 1 eV.
The following link give access to the Web Applications for the Electronic Stopping Power and Dose protons and ions:
- Protons & ions fluence to TID dose converter
How to use this Electronic Stopping Power Calculator and Ionizing Dose Converter
This tool calculates the Electronic Stopping Power curve for a particle incident on a material.
The input parameters and options for the tool are described below. When the input form has been completed, pressing the "CALCULATE" button will start the calculation and open the "Results" page (allow for pop-up in your browser settings). The result page will be also linked at the bottom of the calculator page.
As already mentioned, the current web calculator for electronic stopping powers exploits the "SRIM Module.exe" included in SRIM 2013 code (SRIM Tutorials), whose maximum available energy is 10 GeV/amu. However, an extension up to high Energy for protons and ions in elements and compounds is avaliable within the so called SR-treatment framework (e.g., see the following sr-niel web calculator). Furthermore we recall to the user that, as the incoming particle energy increases, high-energy δ-rays generated in the process of collision energy losses can escape from the absorber (e.g., see webpage).
In the present electronic stopping power to dose converter, the energy lost by the incoming particle is assumed to be fully absorbed by the medium - for instance, the medium is supposed to to be thick enough to fully absorb the kinetic energy of emitted δ-rays - and the particle energy is almost constant while traversing the absorber (e.g., see dedicated webpage).
However, we recall to the user that, as the incoming particle energy increases, high-energy δ-rays generated in the process of collision energy losses can escape from the absorber. Thus, the energy lost by the incoming particle differs from that deposited in the absorber which approches an approximate constant value (the so-called Fermi plateau). This is illustrated, as an example, in the following figure in which the calculated stopping power and measured deposited energy of massive particles with z=1 in silicon are shown for 1< βγ <1000. βγ = 11.61 is that for a proton with kinetic energy of 10 GeV. The sr-niel web calculator accounting for such a physical mechanism is available at this page (see also the corresponding web page within the sr-niel handbook).
 Energy loss in silicon (in units of eV/μm) versus βγ (= p/M0c, where M0 and p are the rest mass and the momentum of the incoming particle with z=1) (see also [Rancoita (1984)]). From the top, the first two curves are: the stopping power without (broken curve) and with (full curve) the density-effect correction (e.g., see Chapter 2 of [Leroy and Rancoita (2016)]) . The red points for incoming protons up to 10 GeV (βγ =11.61) are obtained from present electronic stopping power SRIM calculator implemented in this website. The following two other curves - compared to experimental data for detector thicknesses of 300 (× from [Hancock, James, Movchet, Rancoita and Van Rossum (1983)]) and 900 μm (◦ and • from [Esbensen et al. (1978)]) - are, respectively, i ) the top one (solid line in blue) for the restricted energy-loss with the density-effect taken into account and ii) the bottom one (dashed line in blue) for prediction of the most probable energy-loss. Furthermore (as discussed at page 82 of [Leroy and Rancoita (2016)]), for βγ > 100, in 300 μm thick silicon detector the observed most probable energy-loss (in eV/μm) is about 5% lower than that in 900 μm thick silicon detetor in agreement, within the experimental errors, with the decrease of about 6.5% calculated by means of Eq. (2.56) at page 81 of [Leroy and Rancoita (2016)].
Energy loss in silicon (in units of eV/μm) versus βγ (= p/M0c, where M0 and p are the rest mass and the momentum of the incoming particle with z=1) (see also [Rancoita (1984)]). From the top, the first two curves are: the stopping power without (broken curve) and with (full curve) the density-effect correction (e.g., see Chapter 2 of [Leroy and Rancoita (2016)]) . The red points for incoming protons up to 10 GeV (βγ =11.61) are obtained from present electronic stopping power SRIM calculator implemented in this website. The following two other curves - compared to experimental data for detector thicknesses of 300 (× from [Hancock, James, Movchet, Rancoita and Van Rossum (1983)]) and 900 μm (◦ and • from [Esbensen et al. (1978)]) - are, respectively, i ) the top one (solid line in blue) for the restricted energy-loss with the density-effect taken into account and ii) the bottom one (dashed line in blue) for prediction of the most probable energy-loss. Furthermore (as discussed at page 82 of [Leroy and Rancoita (2016)]), for βγ > 100, in 300 μm thick silicon detector the observed most probable energy-loss (in eV/μm) is about 5% lower than that in 900 μm thick silicon detetor in agreement, within the experimental errors, with the decrease of about 6.5% calculated by means of Eq. (2.56) at page 81 of [Leroy and Rancoita (2016)].
Input Parameters:
- Incident particle (for Protons&Ions Calculator)
- Target material
- Energy of the incoming particle with corresponding fluence
Incident Particle
In the Protons&Ions Calculator, using the pull down menu, the user can select the species of the incident particle, either a proton or one of the elemental ions.
Except for proton and alpha particle mass, the user can also modify the mass (in amu) of the incident particle(e.g., for all isotopes one can refer to this page): the default mass is that of the most abundant isotope (MAI). Further information are available at the following webpage.
Target Material
In the section "Target Selection" it is possible to specify an User Defined target material or a predefined Compound material. User can also select the target as gas, this is allowed only for single element and natural gas target (H, He, N, O, F, Ne, Cl, Ar, Kr, Xe, Rn).
The stopping power in target gases is usually higher than that in an equivalent solid target. The Gas/ Solid correction disappears for higher velocity ions with energies above 2 MeV/amu. But at lower velocities the effect can be quite large - almost a 2 times change in stopping bacause of the Phase effect near the Bohr velocity, 25 keV/amu.
in the User Defined section individual elements can be selected as well as the composition of the target material choosing the number of elements in the compound. The required parameters for each element are:
- Atomic number (Z)/Chemical symbol
- Stoichiometric index or element fraction
Electronic Stopping Power for User Defined Compounds
Electronic Stopping Power for User Defined Compounds can be determined by means of Bragg's additivity rule, i.e., the overall Electronic Stopping Power in units of MeV cm2/g (i.e., the mass electronic stopping power) is obtained as a weighted sum in which each material contributes proportionally to the fraction of its atomic weight. For instance, in case of a GaAs medium ones obtains (e.g., Eq. (2.20) at page 15 in [ICRUM (1993)]):
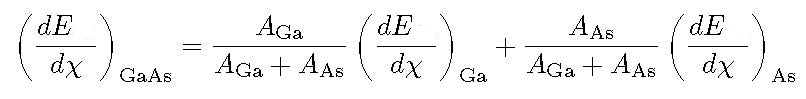
where ![]() and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
and AGa [AAs] are the Electronic Stopping Power (in units of MeV cm2/g) and the atomic weight of Gallium [Arsenic], respectively.
As discussed in SRIM. (see help of "The Stopping and Range in Compounds" in SRIM-2013), the Compound Correction is usually zero for compounds containing heavy atoms, Al(Z>=13) or greater. All experiments with compounds such as Al2O3, SiO2, Fe2O3, Fe3O4, SiC, Si3N4, ZnO, and many more, show less than 2% deviation from Bragg's additivity rule which estimates the stopping by the sum of the stopping in the elemental constituents. That is, the stopping in Al2O3 is the same as the sum of the stopping in 2 Al + 3 O target atoms. For these compounds there is no need for a Compound Correction. This correction should be accounted for in compounds containing mostly H, C, N, O and F for ion stopping below 2 MeV per atomic mass unit and is negligible above 5 MeV per atomic mass unit. In the current calculator, no correction is applied for target atoms lighter than Al. Further details are available at SRIM Compound, and SRIM Compound Theory.
Predefined compounds
In the Compoud section it is possible to select a predefined compound including the SRIM compound corrections in the stopping power calculation.
For instance, in the following plot, it is shown the percentage difference of the stopping power of H2O (selected as User Defined material) and Water_Liquid (selected as a Compound) as a function of the incoming proton energy in MeV: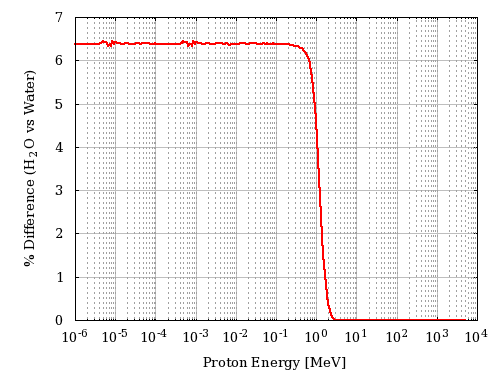
Dose Calculation
This section defines the energy of the incoming particle with corresponding fluence.
The input format is one point per line (Energy - Fluence , separated by a space or tab); it is also possible to copy and paste values.
Use point "." as decimal separator, a space or tab to separate energy value from fluence and use separate raw for adding energy-fluence pair.
Result
The result page contains the input parameters and the result table. For every energy-fluence points the TID dose is calculated in [MeV g-1] and [Gy].